隶属函数法是一种常见的综合评价方法,属于多元统计分析,可用于品种抗性、果实品质、土壤质量等的综合评价。过去常使用平均隶属函数法或者变异系数法与隶属函数结合来进行综合评价,而近年来,主成分分析与隶属函数法结合的综合评价方法的比较流行(其本质是计算主成分综合得分),但初学者往往不知如何操作,本文受有关隶属函数评价法的应用感想帖子和SPSS隶属函数分析主成分分析相关性分析经验分享(其中存在错误)视频的启发,以spss和excel为工具,用图文的方式详细描述了该方法的具体步骤,希望能对大家有所帮助。
导入数据
数据以均值的形式,导入spss中。(这里理应样本数>变量数,但博主偷了懒,数据构造的不合理,导致spss提示不是正定矩阵,KMO与bartlett检验显示不出来)
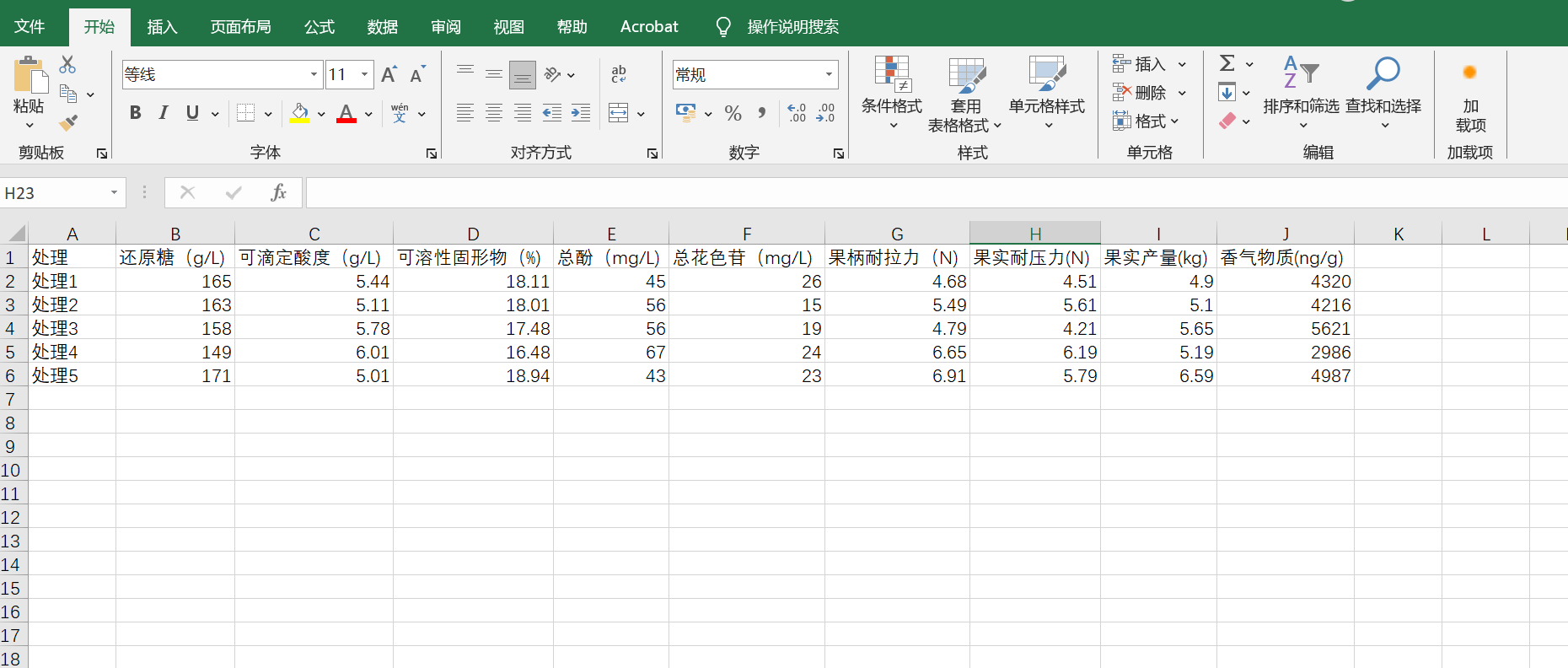 | 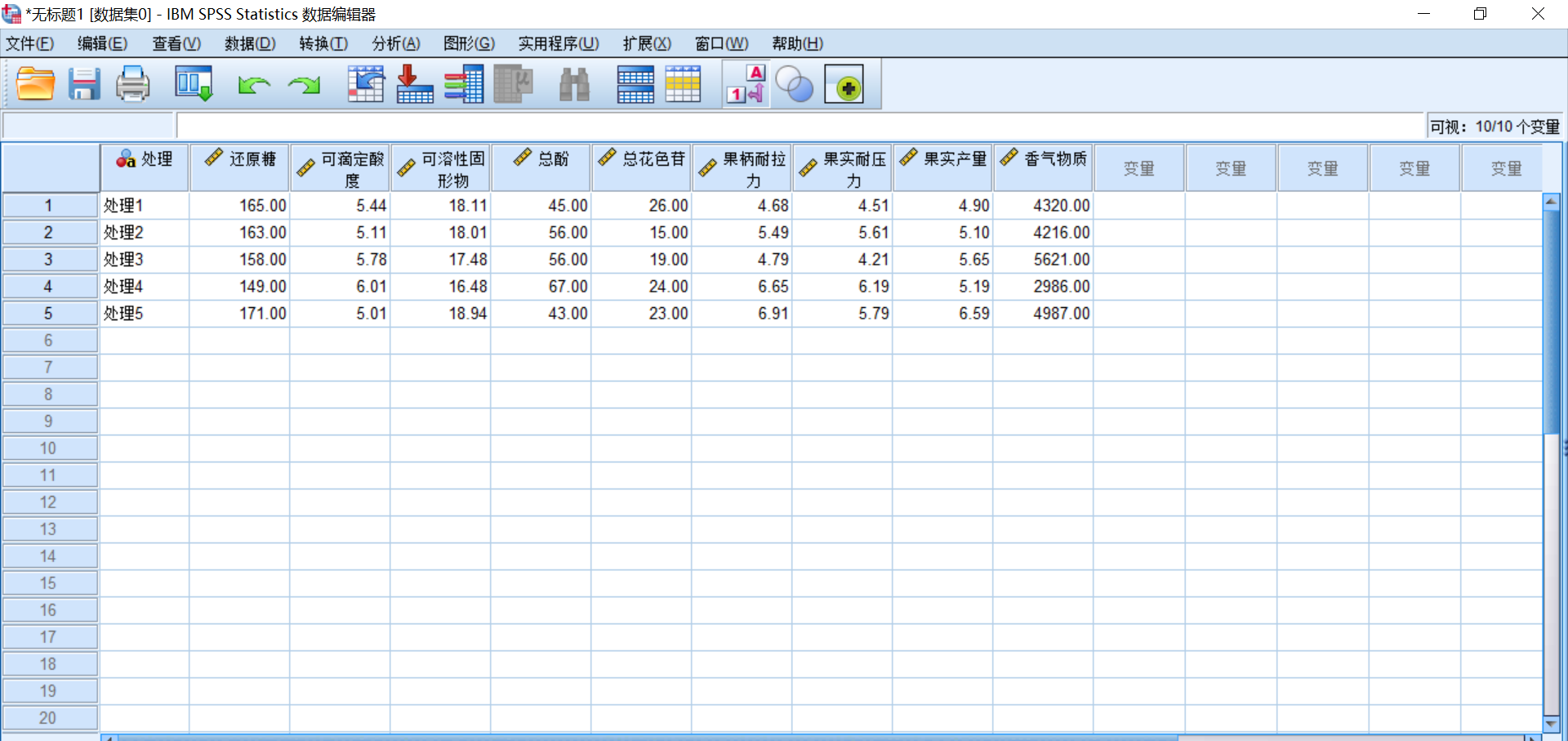 |
数据分析
先使用spss对数据进行主成分分析
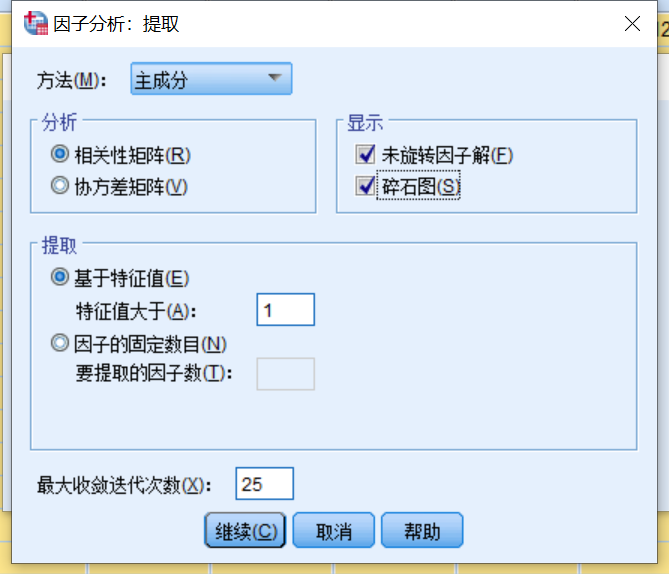
点击spss上方的“分析”→“降维”→因子,将指标全移入到变量栏,然后按下图勾选必要的选项进行数据分析。
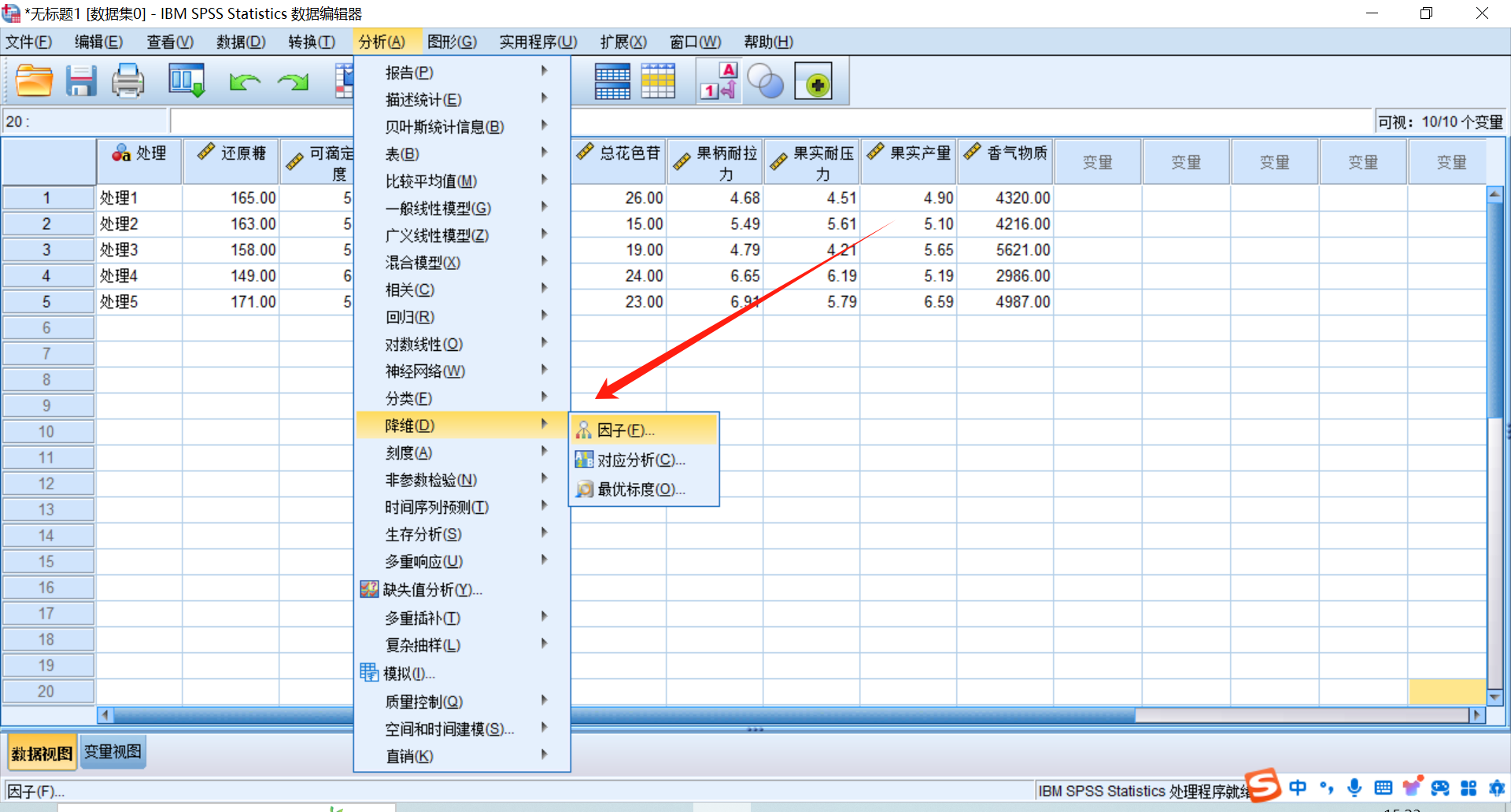 | .jpg) |
 |  |
 |  |
| |
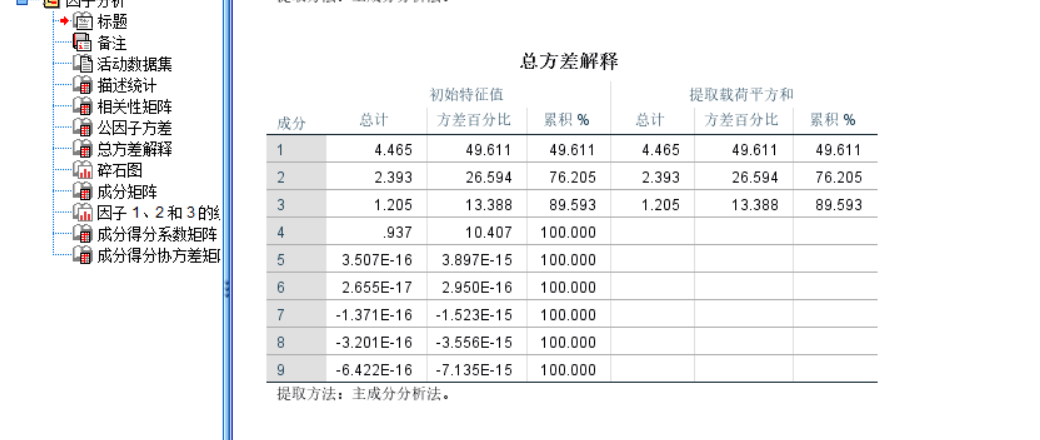
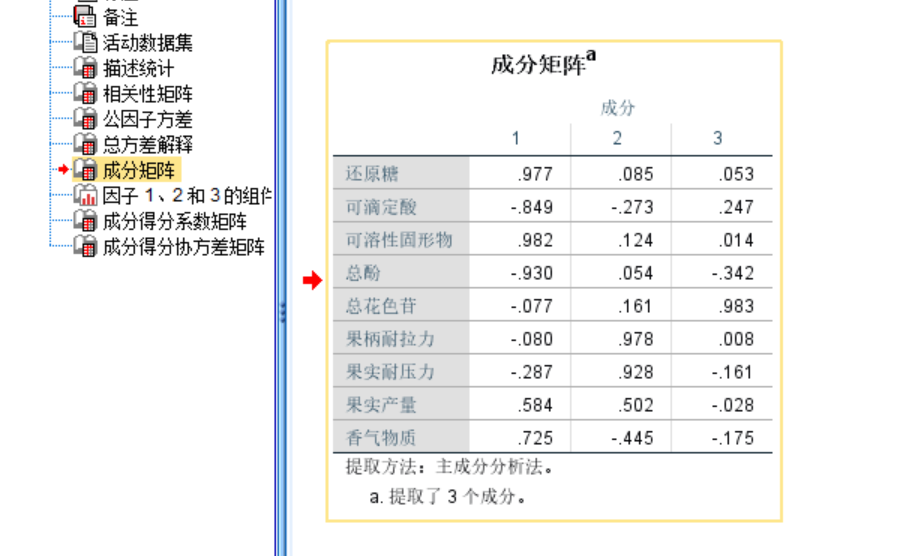
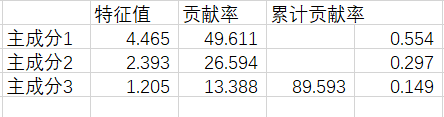
首先要看KMO与bartlett检验的结果,如果KMO≥0.5且bartlett检验显著性<0.05,则主成分分析可以继续进行,如果只通过一个检验,则可以观察提取主成分的累积方差贡献率,如果足够高那也是可行的,没通过检验的可以适当调整数据以通过检验,如删减相关性高的变量,数据无法调整的建议改用其他分析方法。主成分分析的关键数据,主要看“总方差解释”和“成分矩阵”,这里以特征值大于1,且累计方差贡献率大于80%的标准(其实没有固定标准)来选择主成分个数。本次分析中前三个主成分的特征值均大于1,累计贡献率达89.573%,满足标准。如果出现累计贡献率大于80%,而特征值小于1,或者特征值大于1,但累计贡献率不足80%的情况,可以主动选择提取主成分的个数,满足标准,即再进行一遍上述的主成分分析操作,其中只需按下图改变“提取”的选项,然后获得新的结果。
 |  |
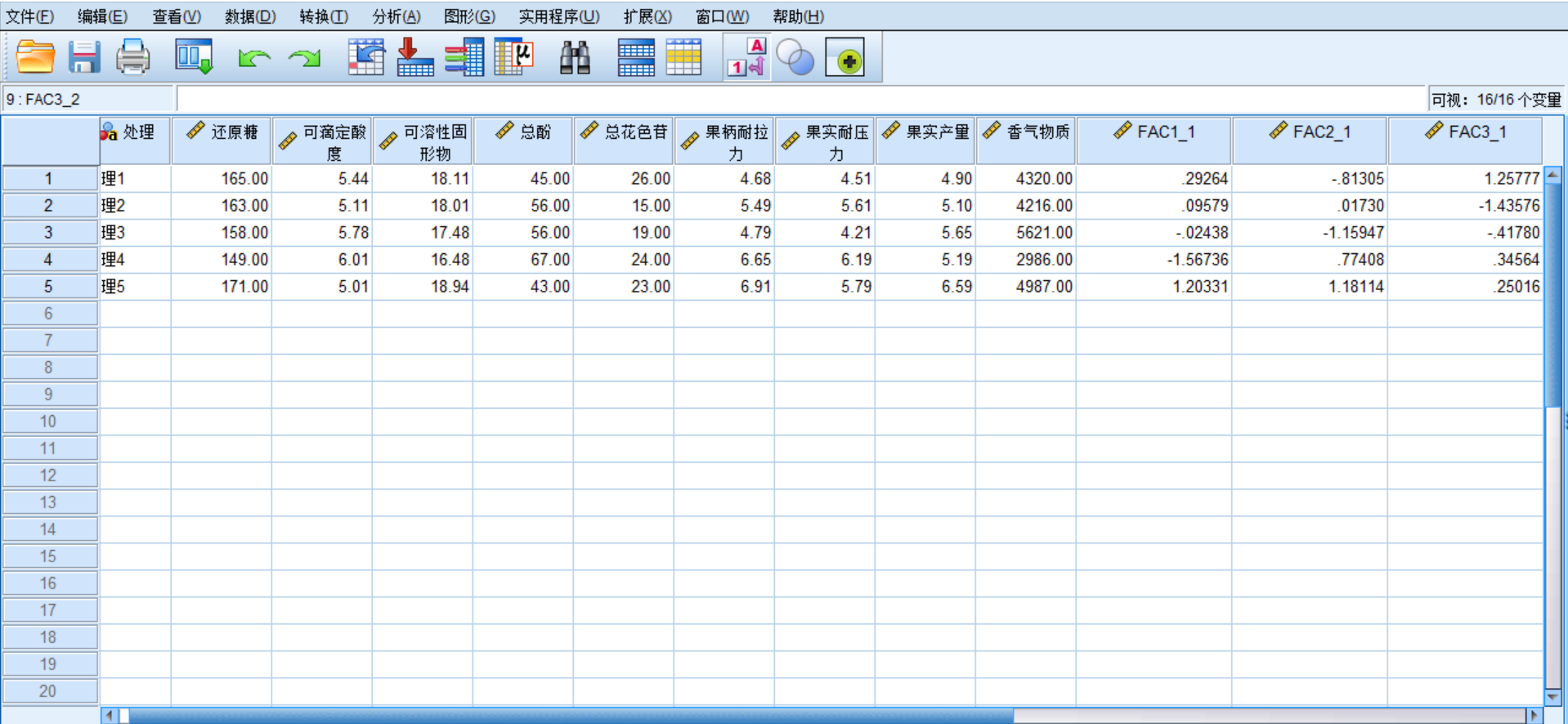 | |
因为我们执行的是SPSS因子分析程序,所以SPSS计算的因子得分(FAC1_1~FAC1_3)是不能用于主成分分析上的,我们需要重新计算。这是一个SPSS很大的缺点,不能直接进行主成分分析,也因此导致初学者乃至很多人将主成分分析和因子分析弄混(也是很多b站教学视频存在的问题),分不清主成分和因子分析的得分系数,这里参见文献(林海明,张文霖.主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J].统计研究,2005,(03):65-69. 和马娟,杨益民.主成分分析与因子分析之比较及实证分析[J].市场研究,2007,(03):30-34.),将问题讲解的十分明白了。
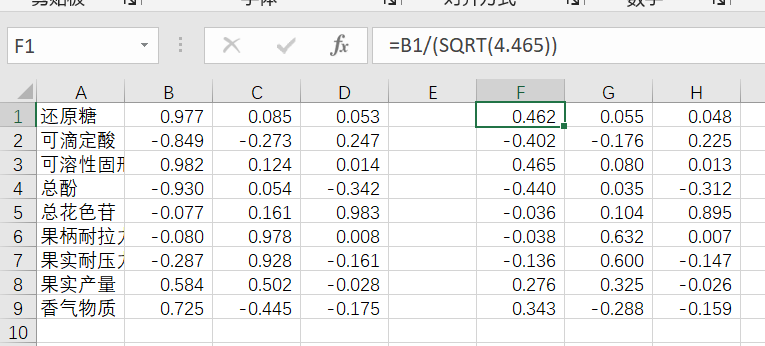
接下来将成分矩阵的数据复制到Excel表中,计算主成分得分系数矩阵,公式为各成分的载荷除以各成分对应的特征值的算术平方根,即A/(sqrt(λ)。
|
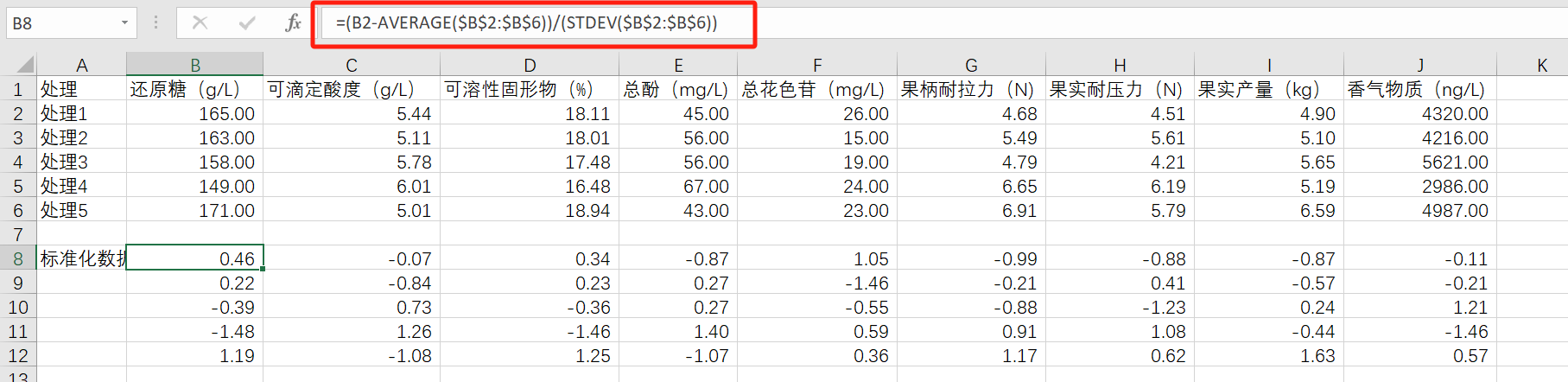
然后将其与标准化后的原始数据相乘(标准化公式为(X-μ)/σ),得到各主成分得分F1、F2、F3,这里还需我们在Excel中对原始数据进行下标准化处理。
 |  |
更简单的是将spss的因子得分结果乘以对应主成分特征值的算术平方根,一步到位,见下图
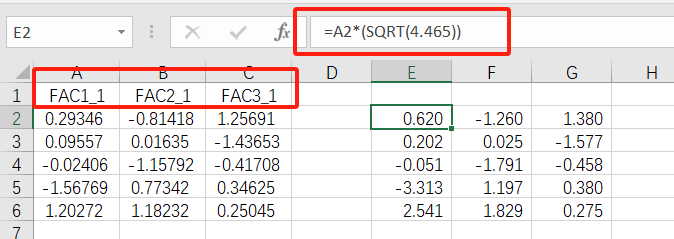
这里与下文的得分计算在第三位小数上存在差异,是因为代入数据小数保留位数的原因,保留2位小数不影响结果
再根据权重计算主成分综合得分,这里权重计算公式为各主成分贡献率除以提取主成分的累计贡献率,最后进行排序,到这其实已经是一个完整的主成分分析了。
 | 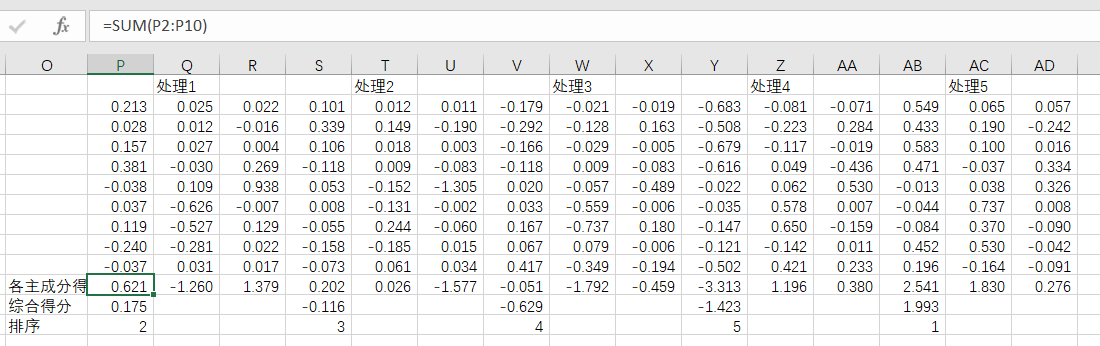 |
主成分得分
那么我们怎么引入隶属函数呢?从多数文献上来看,隶属函数用在了F1、F2、F3各主成分得分上,即将各主成分得分进行了隶属函数化(其实就是归一化),然后引入权重,按照主成分综合得分公式计算综合得分。从这来看,主成分综合得分和隶属函数得分的结果其实没有区别,只不过得分数不一样(隶属函数化后分数在0-1区间,看起来美观),但排序结果是相同的。然后根据隶属函数法的公式进行计算,最终得出D值,即综合评分的数值。
同时也有另外一种引入隶属函数的方式,即先进行隶属函数化再主成分分析,而上一种则是先主成分分析再隶属函数。具体操作就是先将原始数据进行隶属函数化,对于负向指标就反隶属函数化,而对于有阈值的指标则可以分段使用公式(比如还原糖的含量设定为0-220范围内就是越高越好,则使用正隶属函数化,而超过220这个阈值越高越不好,则使用反隶属函数化),然后以隶属函数化的数据再进行主成分分析(这里不用再进行标准化操作,避免信息损失),计算综合得分。
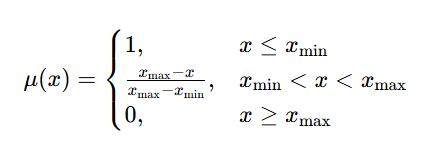
这种算法最适用于指标量纲不统一、正负向混杂、线性关系分明的场景,比如锂电池正极材料性能评估,比容量、充放电效率与循环寿命为正向指标、粒径分布为适中型指标、杂质含量为负向指标。但这种算法在文献中报道较少,不常见,与之类似的有TOPSIS法,但其应用非常广泛。
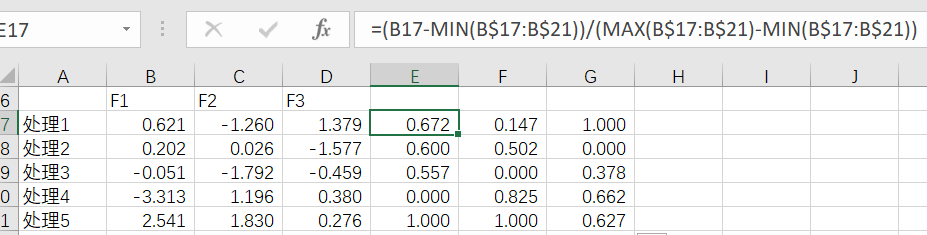 |  |
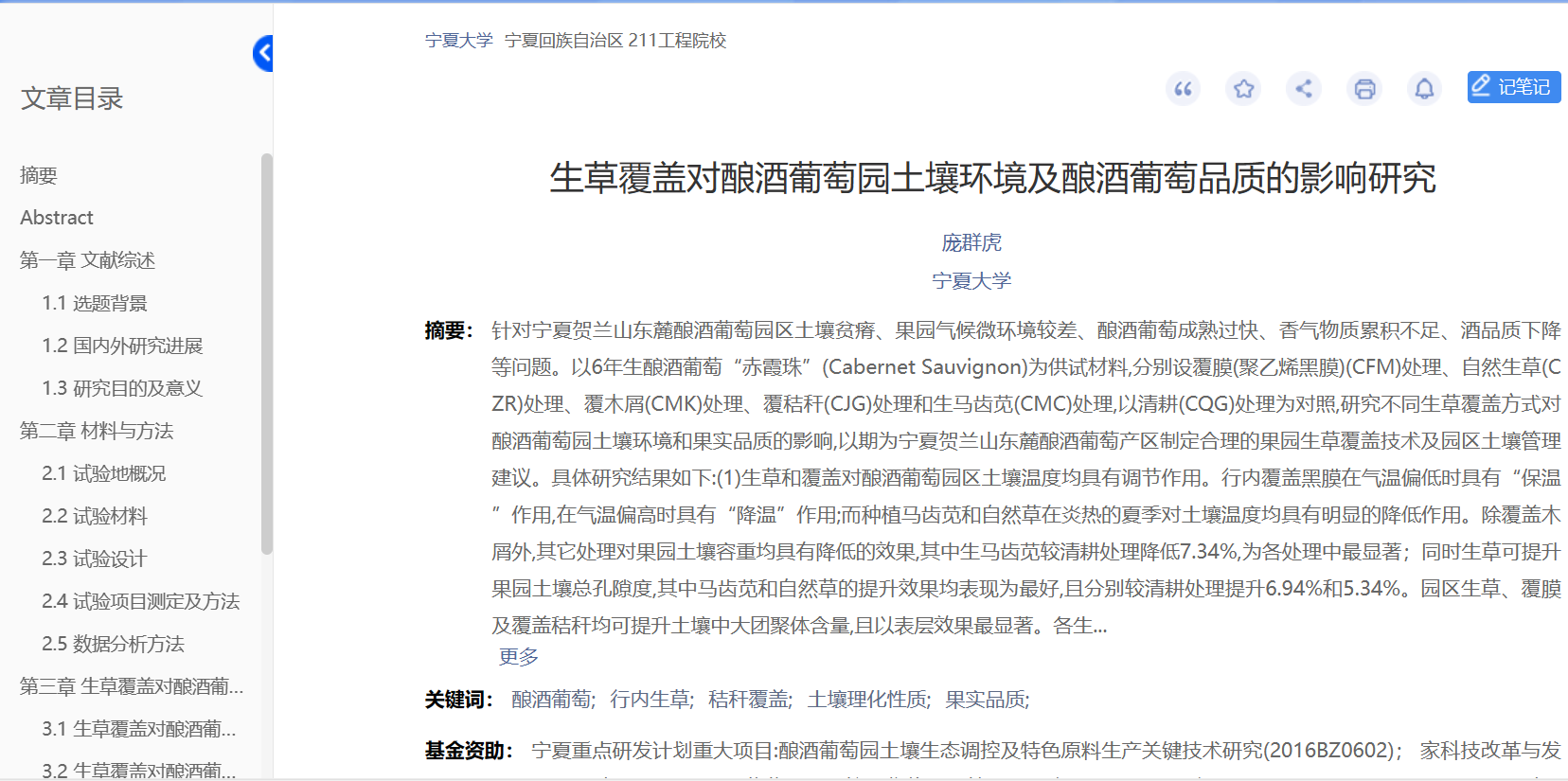 |  |
文献示例
关于方法文献的引用参考:Xingfan Li, Shakir Ullah, Ning Chen, et al. Phytotoxicity assessment of dandelion exposed to microplastics using membership function value and integrated biological response index, Environmental Pollution, Volume 333, 2023, 121933.或者张斌斌,沈志军,马瑞娟,等.基于果肉单体酚和总酚含量评价桃果实抗氧化能力[J].园艺学报,2018,45(05):931-942.
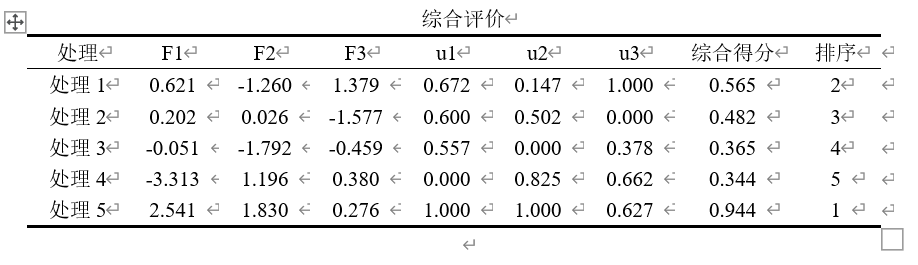
结果
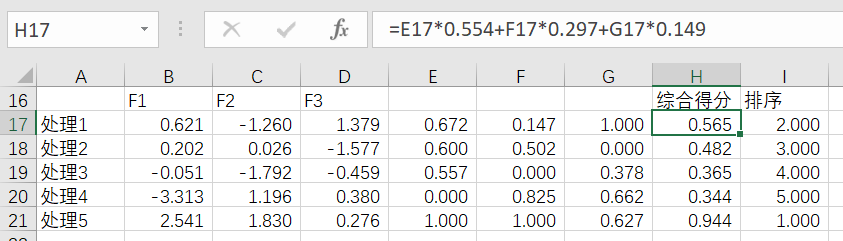
最终的结果如下图所示,可以放在论文中。主成分表达式y1、y2、y3中的每一项x的系数分别对应主成分1、2、3的成分得分系数(见上面Excel表中的F1、F2、F3),总表达式的各项系数对应w1、w2、w3(即各主成分的贡献率与总累计贡献率的比值,权重),综合得分F=w1*F1+w2*F2+w3*F3=0.554*F1+0.297*F2+0.149*F3。
 |  |
 | |
以上就是全部内容,如有疑问,欢迎大家在评论区交流讨论!
教程制作不易,看完点个赞鼓励下博主吧!

参考资料:
SPSS因子分析中成分矩阵、旋转成分矩阵和成分得分系数矩阵的区别_成分矩阵和旋转成分矩阵的区别
林海明,张文霖.主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J].统计研究,2005,(03):65-69.
马娟,杨益民.主成分分析与因子分析之比较及实证分析[J].市场研究,2007,(03):30-34.
庞群虎.生草覆盖对酿酒葡萄园土壤环境及酿酒葡萄品质的影响研究[D].宁夏大学,2019.DOI:10.27257/d.cnki.gnxhc.2019.000869.
苏小雨,高桐梅,张鹏钰,等.基于主成分分析及隶属函数法对芝麻苗期耐热性综合评价[J].作物杂志,2023,(04):52-59.DOI:10.16035/j.issn.1001-7283.2023.04.008.




博主,我按照你上一篇关于主成分分析的方法算出了主成分的得分,这个得分就是隶属函数的综合得分吗?
用这篇的方法就行,这个就是主成分结合隶属函数的综合得分,文献也有相关报道。
您好,我想问一下,我的实验是对三个品种五个温度胁迫下测量了六个生理指标,对这三个品种进行隶属函数分析但是不知道这五个温度如何处理,求解
你是每个品种都做了五个温度胁迫吗?如果是这样的话,那就是15组,然后统一进行隶属函数分析。
是的我每个品种都做了五个温度胁迫,但是按15组分析的话得到的就是品种*温度的分析,我只想要分析出哪个品种抗逆比较好,是不是应该求平均值,但具体应该怎么做呀,求解!
温度的抗逆性又分为抗旱与抗寒,我建议分开来评价,比如在最低温度下胁迫的5个品种做一次主成分综合得分,得到抗寒性排名,最高温度又做一次,得到抗旱性排名,综合来看哪个品种抗旱与抗寒排名都比较靠前。
您好!请问有排序那张图中的综合得分是主成分得分的总和吗?算了几遍不明白综合得分是怎么算出来的,求您解答
综合得分是各主成分的加权之和,文中倒数第三张图里面有计算公式,y=w1*f1+w2*f2+w3*f3=0.554*f1+0.297*f2+0.149*f3。
感谢答复!我想请教的是倒数第五张图中的综合得分0.175是怎么算的,是算PQR列2-10行的总和,在用三个总和求总和得来的吗?
不是,还是按综合得分公式计算的,即y=w1*f1+w2*f2+w3*f3=0.554*0.621-0.297*1.26+0.149*1.379=0.175
然后还有一个问题是标准化的时候可以按照b站上他们直接用spss软件,描述功能里里标准化吗?感谢分享。
可以的,spss自带标准化功能。
你好,就是最后一步的话,F1,F2,F3的系数的话,就是拿之前那个百分比除以它的累计百分比吗?我是想得到一个综合的评价方程f总。
是的,就是计算权重,拿各主成分贡献率除以选择主成分的累计贡献率。
你好,我搜索很多文献结合AI问答,发现您这种计算方法会不会偏老了。
在PCA中,得分是通过将标准化后的原始数据与特征向量(即成分得分系数矩阵)相乘得到的。
SPSS中保存的FAC1, FAC2等变量正是这样计算出来的,因此它们是主成分得分。尽管变量名以FAC开头,只要抽取方法是“主成分”,它们就是主成分得分。
在SPSS中执行主成分分析(PCA)时,当我们在“得分”部分勾选“保存为变量”,生成的变量(如FAC1_1, FAC2_1等)实际上就是主成分得分,而不是因子分析中的因子得分。SPSS的因子分析同时包含主成分分析(PCA)和公因子分析(FA)两种方法。当我们在“抽取”方法中选择“主成分”时,执行的就是PCA;如果选择其他方法(如“主轴因子法”),则是FA。
我这个也是乱了好久,希望您看到后有空回复我您的意见,谢谢!
林海明,张文霖.主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J].统计研究,2005,(03):65-69. 和马娟,杨益民.主成分分析与因子分析之比较及实证分析[J].市场研究,2007,(03):30-34.),这两个文献太老了,spss都更新到27.0了,这个问题应该搞定了。
你好,在PCA中得分是通过将标准化后的原始数据与特征向量(即成分得分系数矩阵)相乘得到的是没错,但是spss中直接得出的成分得分系数并不是真正的主成分得分系数,需要进行公式转化(本文中也提到了),所以直接得出的FAC1_1等也不正确,不等于主成分得分。
这些与spss的版本没有关系,是主成分与因子分析得分系数使用的公式不一样所导致的。,我使用spss27.0、origin、spssau再次验证了一下,发现结果与本文中都是相符的,spss与origin的结果见网站的另两篇文章“使用Origin完成主成分分析并绘图”“SPSS——详解主成分分析(PCA)与因子分析(FA)”,spssau的结果也是一致的,方法与文献并没有过时。在SPSS中,“抽取”方法并不是主成分分析与因子分析的根本区别,“主轴因子法”只是因子分析中的一种因子选择方法,因子分析也能使用“主成分”抽取。真正的区分应该是“旋转”这一步,主成分分析是不需要进行因子旋转的,而因子分析可旋转可不旋转,所以只要是进行旋转了肯定是因子分析。如果你还有更多问题,可以加我的qq445684710(同邮箱)进行交流。
作者综合得分怎么算的呢
综合得分等于各主成分得分乘以各自的权重的总和,即D=u1*w1+u2*w2+...un*wn,权重w的计算方法文中有提到。
天呐 太有用了,跟着做一遍就差不多懂了,太感谢博主了,真的太感谢了
太有用了,跟着做一遍就差不多懂了,太感谢博主了,真的太感谢了
请问一下要是处理里面有五天的数据,该怎么计算呢
你的意思是同一个处理,然后连续测了五天的数据吗?那根据你的研究目的,可以单独拎出来作为一个分组(5天分为5组),进行纵向对比。可以描述的更详细一点哈。
然后我还看到有的教学是用SPSS进行标准化处理,步骤是:分析——描述统计——描述,在弹出的窗口栏你勾选“讲标准化得分另存为变量”,然后SPSS会在原始数据表后面多生成Z开头的测量标度,这个处理出来的数据结果和我上一条回复所说的两种计算方法结果又不一样,不知道这个方法能不能用来进行标准化处理?还望您高见
我试了一下,是与(X-X平均值)/X标准差公式一致的,能用来进行标准化处理。
您好,请问标准化怎么计算呀,我看有的教学是用(X÷Xmin)÷(Xmax-Xmin)说这个算出来的值就是标准化,您这里是用(X-X平均值)/X标准差,看头晕了,我不知道应该用哪个😣
你好,前一个是归一化,后一个才是标准化,详见https://blog.csdn.net/ytusdc/article/details/128504272
那我是选择归一化还是标准化呢?我归一化之后还需要进行标准化吗?
主成分分析采用的是标准化处理
您好,文中写到了“特征值>1,但累计贡献率不足80%,可以主动选择因子个数,满足条件”,这是要怎么操作呢,要怎么确定因子个数呢,怎么算满足条件呢,求解
一般是以“累积贡献率>80%”为标准来选择主成分个数。假如我特征值>1的主成分只有2个,其累积贡献率为60%,但为了满足80%的标准,我将特征值<1的主成分也一并提取,刚好前4个主成分满足要求。那么我们需要在spss中重新进行主成分分析操作,在其中“提取”选项中,将“基于特征值”改成“因子的固定数量”,这里我需要提取4个主成分,于是设定为“4”,其他操作不变,这样呈现的结果就是我们所需要的。
主成分1特征值不是4.463吗?怎么计算的时候变成4.465了
是的,感谢指正。一时疏忽后面代错了,不过不影响结论哈 ,后续会进行纠正。
,后续会进行纠正。
没有,没有,楼主做得很好了
您好,PCA分析不需要计算KMO吗?
不需要,因子分析才需要计算KMO。
您好,请问负相关的指标,该在哪一步用1-隶属函数这个公式呢?
你好,我查阅了很多文献发现有两种计算方式。
一个是本文所写到的,不考虑单个指标的正负相关性,直接通过主成分分析提取了主变量,再以此计算隶属函数值,获得综合评分。
另一个则是考虑单个指标的正负相关性,可以参考https://www.bilibili.com/video/BV1rt421F7AP这个视频的步骤操作,文献可以参考 袁嘉玮,王璐,张茜茹,等.采前喷施氯化钙对苹果叶片光合功能和果实品质的影响[J].江苏农业科学,2023,51(20).基本流程是先对原始数据按照隶属函数或者反隶属函数公式(即你所说的1-隶属函数)计算得分,这里什么时候采用反隶属函数公式,一是可以自己事先拟定,比如在评价果实品质时,认为可滴定酸度越小口感越好,或者糖酸比0-30时口感是越高越好,30是最好的,而超过30以上是越高越不好,这些都是可以人为设定的;二是自己判断不准,则是可以通过相关性分析判断指标的正负相关性,来决定是采用隶属函数公式还是反隶属函数公式。计算完隶属函数值后,再将这些值代入到主成分分析的主成分得分公式(F1,F2,F3...),最后计算综合得分F(F=xF1+yF2+zF3)。
至于这两种方法的区别,前一种更像是套了隶属函数法皮的主成分分析,其本质是主成分分析,只是以隶属函数的形式呈现了结果而已(将综合评分控制在0-1区间),后面不进行隶属函数转化,直接代入主成分得分公式得到的排名结果是不变的。后一种则是以隶属函数法为核心,先将原始数据代入隶属函数公式得到单因素隶属度,再通过主成分分析计算各原始指标的权重,然后得到综合隶属度,即综合得分。
你好,请问一下这两种方法计算出的结果会不会不一致呢,两种方法对于计算结果的区别在哪里?因为我自己计算了一下,最终得分和排名都有所差异。
文献上很多都用的第一种方法,第二种比较少,只有少数几篇文献有报道,我个人觉得第二种计算方法有待商榷(主成分分是将原始数据标准化,而隶属函数是将原始数据均一化),第一种是完全没问题放心用的,因为其本质是主成分综合得分。其实在很多文献中,隶属函数法常和变异系数法结合使用,过去也常使用平均隶属函数得分(均权),但现在基本不采用这种方法了。稳妥起见,还是第一种方法更好。
计算u1,u2...un时使用
u1,u2指的是f1、f2吗
是的
主播,请问用这种方法计算出来,在文章里的试验方法应该如何描述
主播,请问用这种方法计算出来,在文章里的试验方法应该如何描述
引用文献参考10.1016/j.envpol.2023.121933或者张斌斌,沈志军,马瑞娟,等.基于果肉单体酚和总酚含量评价桃果实抗氧化能力[J].园艺学报,2018,45(05):931-942.