主成分分析与因子分析都能用于数据的降维,来综合评价或分析某事物的好坏或变化规律,这均可通过SPSS软件来实现。但由于种种原因,网上许多教学视频、期刊论文中混淆了主成分分析与因子分析的使用方法,出现“以讹传讹”的现象。本文从应用操作的角度,通过SPSS详细介绍了主成分分析与因子分析的具体操作方法,希望对各位的工作学习能有所帮助。
主成分分析(Principal Component Analysis,简称 PCA)是一种统计方法,主要用于数据降维,同时尽可能保留原始数据的关键信息。它的核心思想是通过线性变换将高维数据转换为少数几个相互独立的主成分(新变量),这些主成分能够反映原始数据的变化信息。主成分分析追求在降低变量数量的同时最大保留原始信息(方差最大化),创造了新变量,不强调变量的可解释性,常用于自然科学领域,进行数据的压缩降维。
分析的前提条件:样本数≥变量数,样本数越多越好,如果样本数≤变量数,会出现模型过拟合,信息失真,解释性差等问题;最好通过KMO与Bartllet检验,KMO≥0.5(0.7以上最佳),Bartllet检验p<0.05,不通过则可能出现解释度差、无法有效降维等问题。
因子分析(Factor Analysis,FA)也是一种降维方法,但主要目标是从多个观测变量中提取少数几个潜在的、不可直接测量的 “公因子”,用于解释原始变量之间的相关性。因子分析是寻求能够解释多个指标的独立公因子,公因子具有可解释性,可以帮助我们理解潜在变量间的因果关系/相关性,常用于人文社科领域,进行理论或假设的验证。
分析的前提条件:样本数远大于变量数(样本数≥50,且是变量数的5倍以上),样本数越多越好,且要通过KMO与Bartllet检验,KMO≥0.5(0.7以上最佳),Bartllet检验p<0.05。如果样本数小于变量数,不会通过KMO与Bartllet检验,也就不适合进行因子分析。
| 主成分分析 | 因子分析 | |
| 主要目标 | 最大化方差解释,压缩数据降维 | 解释变量间的协方差,找到潜在公因子 |
| 假设条件 | 样本数≥变量数 | 变量需服从正态分布、连续、相关性强等条 件,样本数远大于变量数,且通过KMO与Bartllet检验 |
| 可解释性 | 主成分无明确语义(PC1) | 公因子存在实际意义(如“理综成绩”) |
| 还原性 | 强,主成分是原始变量的精确的线性组合 | 弱,仅解释公共部分,忽略特殊因子 |
| 应用场景 | 数据压缩、去噪、可视化 | 理论模型的假设验证 |
SPSS主成分分析操作
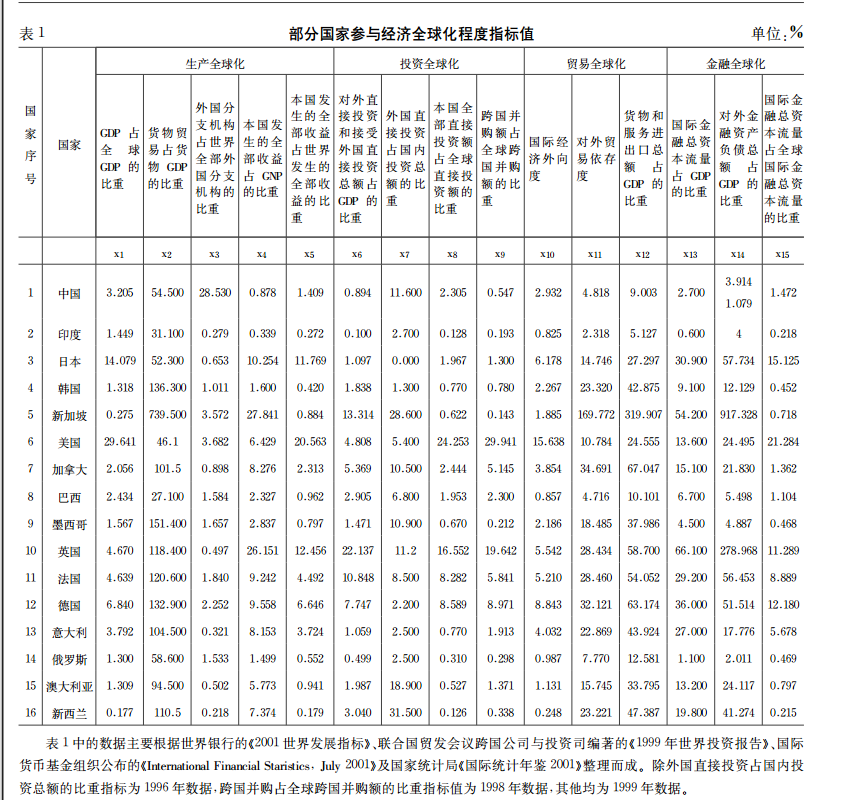
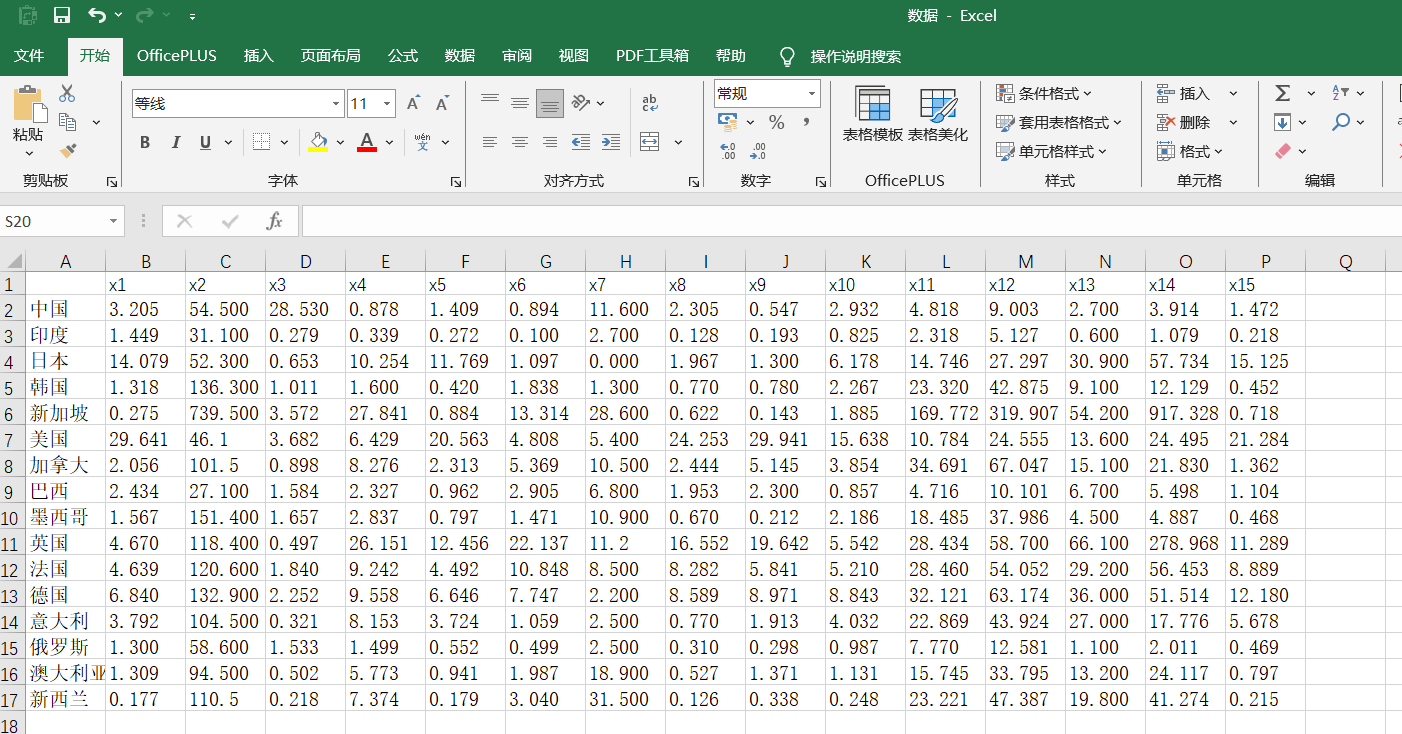
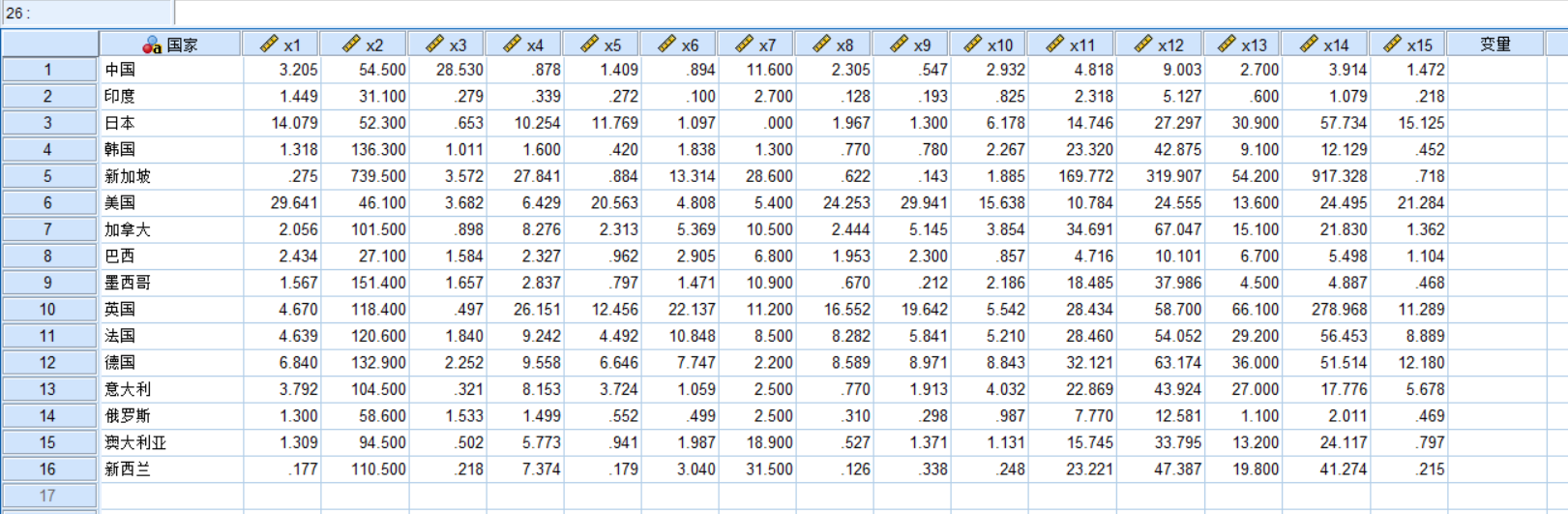
数据来源于论文《经济全球化的量化研究》——刘玉玫,共16个样本,15个变量,导入到SPSS中。
 | |
 |  |
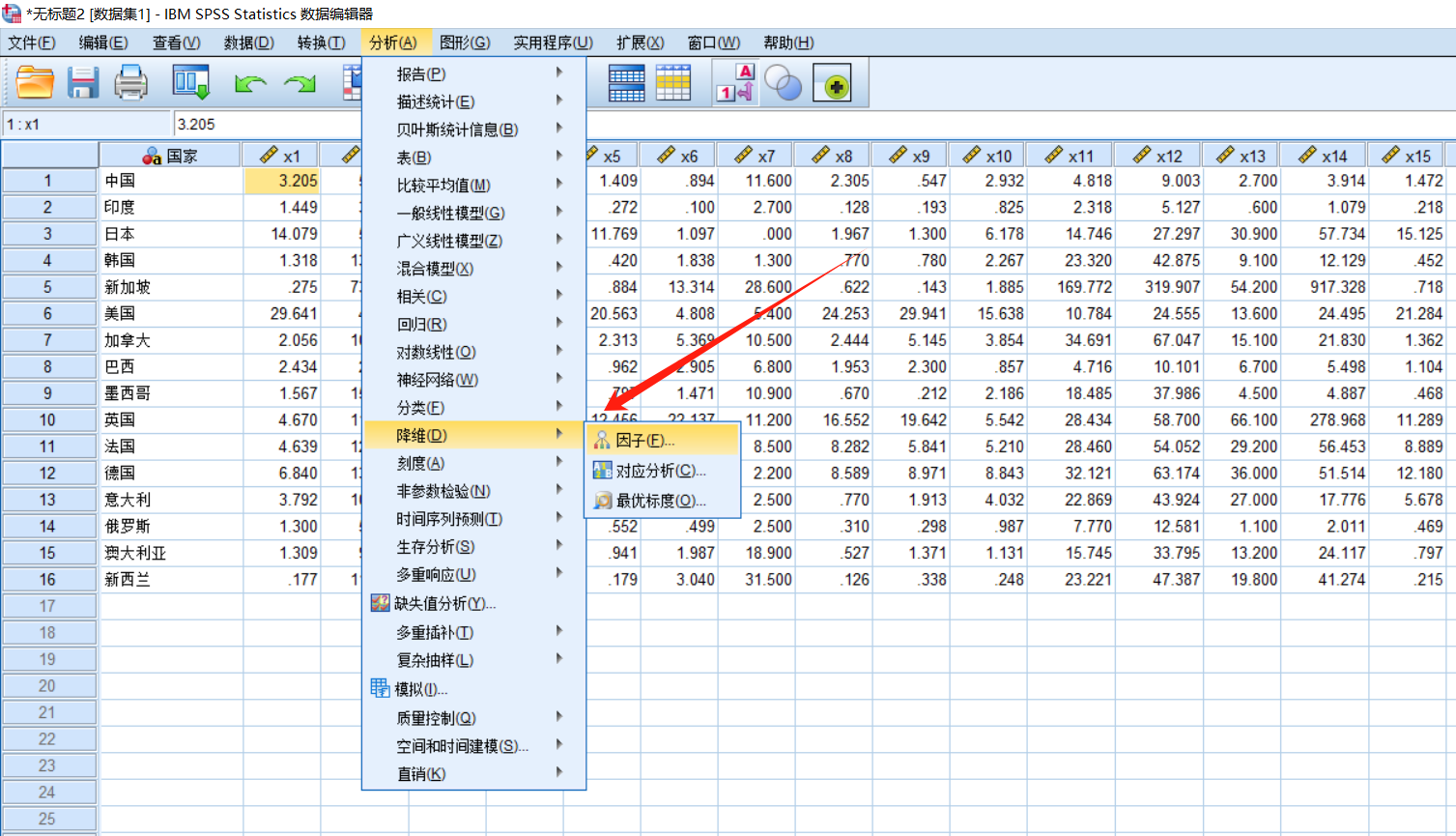
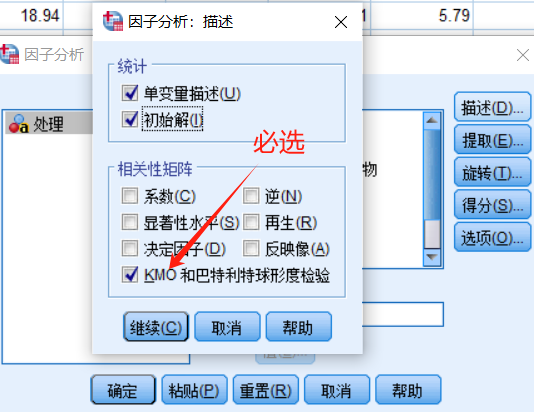
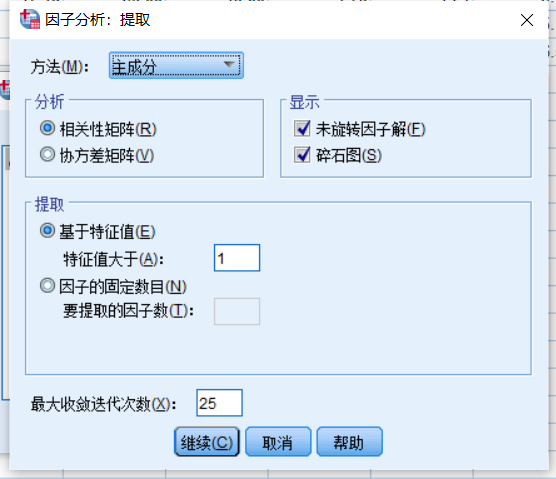
点击spss上方的“分析”→“降维”→因子,将变量全移入到变量栏,然后按下图勾选必要的选项进行数据分析。
 |  |
 | .jpg) |
 |  |
.jpg)
首先看KMO与Bartllet检验,这里KMO<0.5,但通过了Bartllet检验,且公因子方差都接近1,提取的主成分累积方差贡献率高,变量表达较好,表示可以进行主成分分析。
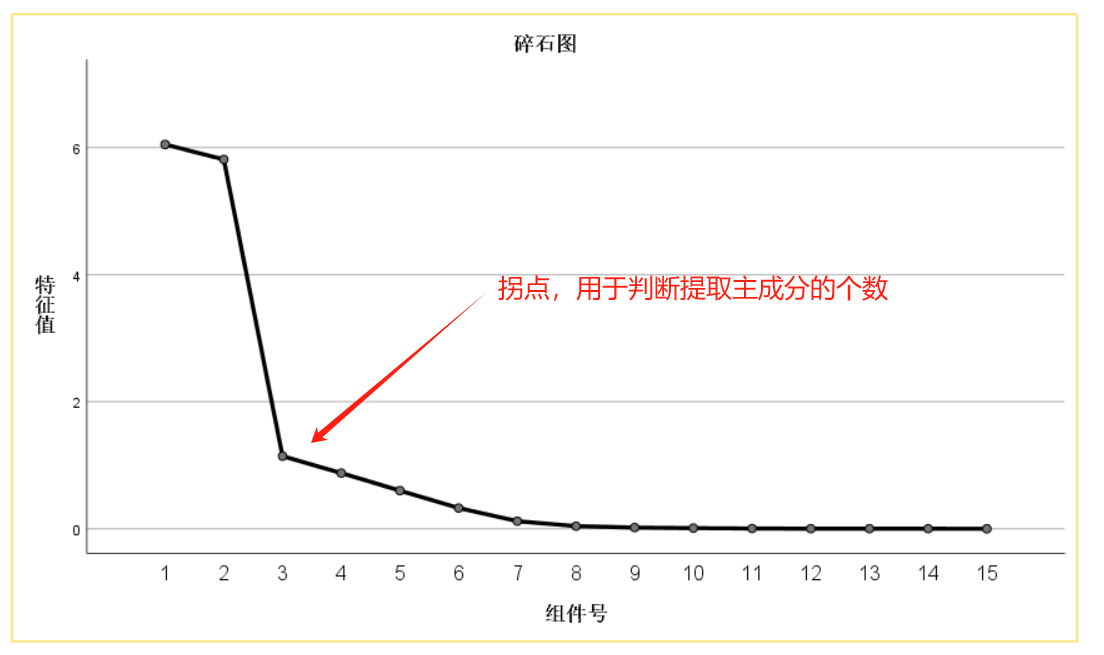
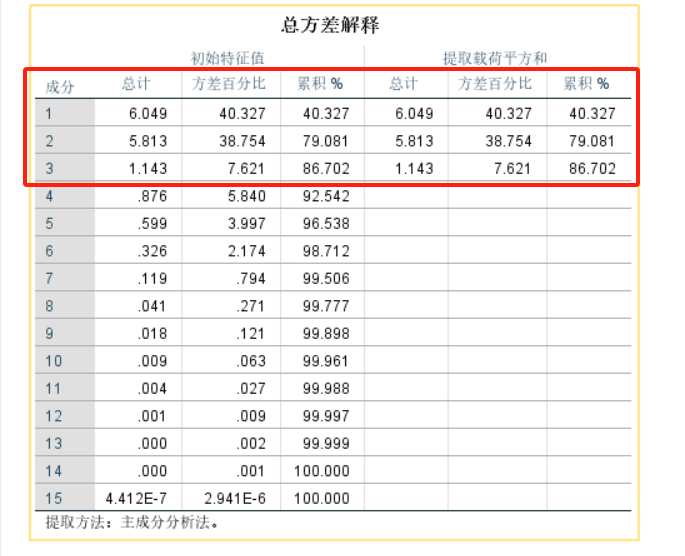
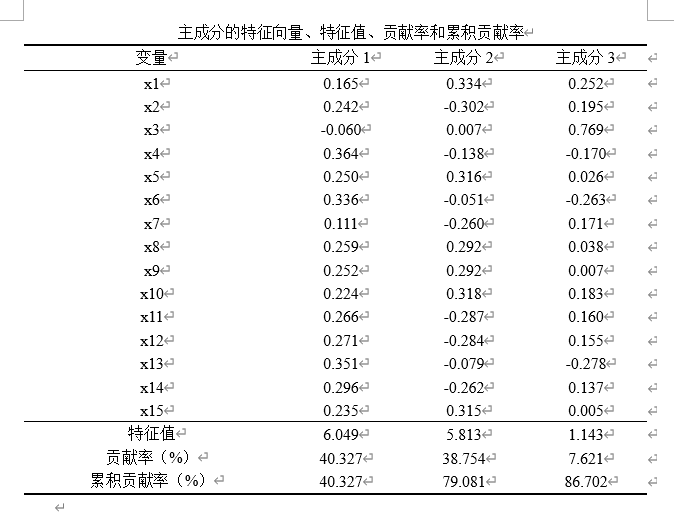
提取主成分分析后的有用数据,主要看“总方差解释”和“成分矩阵”,这里以特征值大于1且累计方差贡献率大于85%的标准(标准不固定,一般建议累积方差贡献率在85%以上,特征值大小为次要条件)来选择主成分个数。如果提取主成分的累计方差贡献率过低,可以再进行一次主成分分析操作,在“提取“选项中选择“因子的固定数目”,然后自行确定主成分个数来完成主成分分析。本次分析中前三个主成分的特征值均大于1,累计贡献率达89.573%,满足标准。碎石图也可以作为辅助手段,以“拐点”来选择主成分个数。
 | .jpg) |
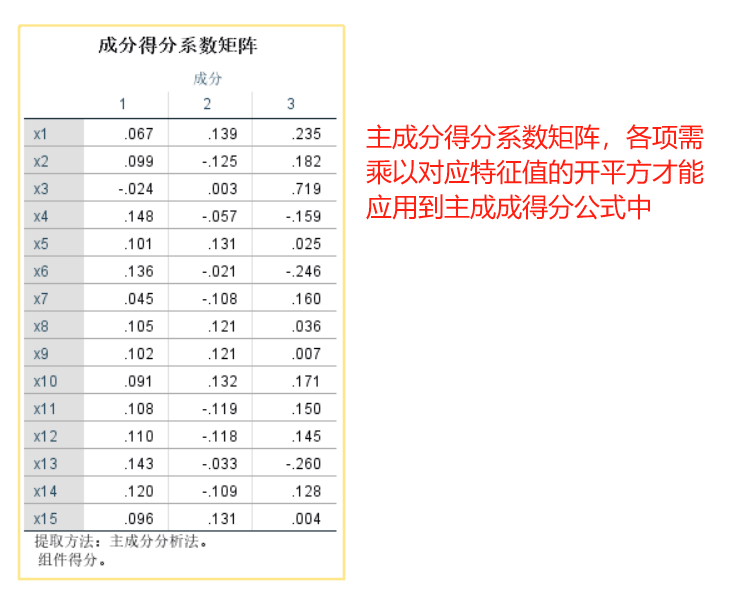 | 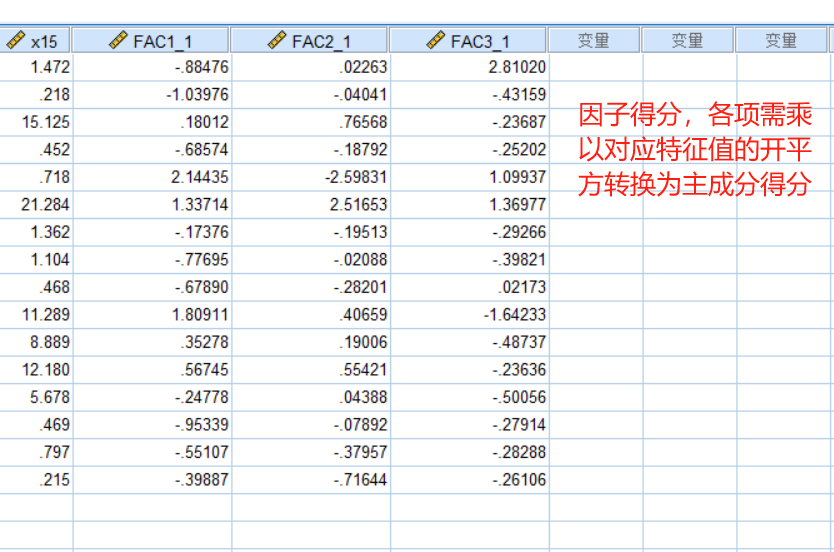 |
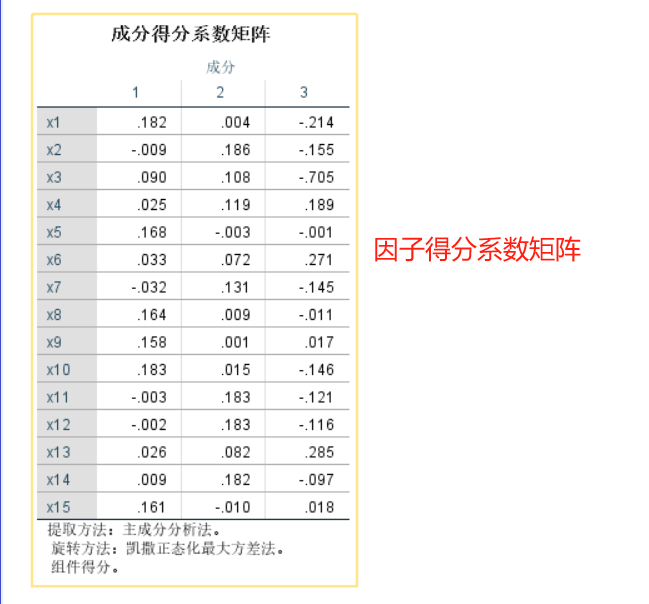
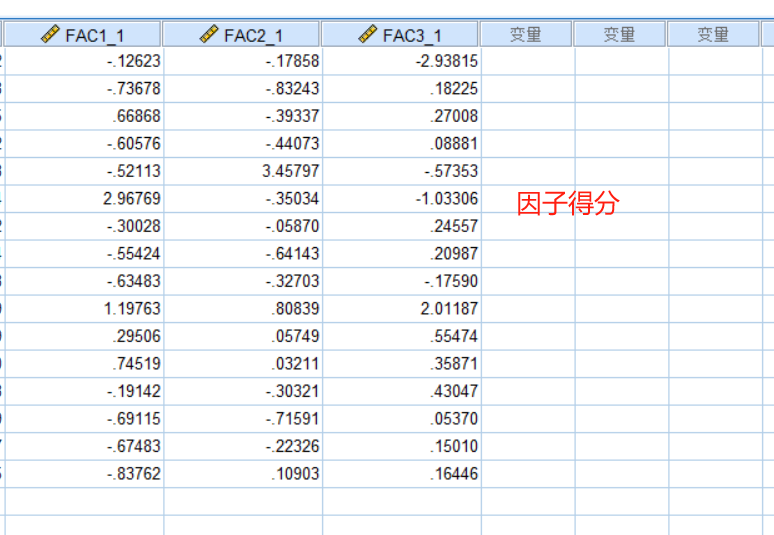
因为我们执行的是SPSS因子分析程序,所以SPSS计算的成分得分系数矩阵与因子得分(FAC1_1~FAC1_3)是不能直接用于主成分分析,需要重新计算。这是一个SPSS很大的缺点,也导致初学者乃至很多人将主成分分析和因子分析弄混(也是很多b站教学视频存在的问题),分不清主成分和因子分析的得分系数,这里参见文献(林海明,张文霖.主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J].统计研究,2005,(03):65-69. 和马娟,杨益民.主成分分析与因子分析之比较及实证分析[J].市场研究,2007,(03):30-34.),将问题讲解很明白了。
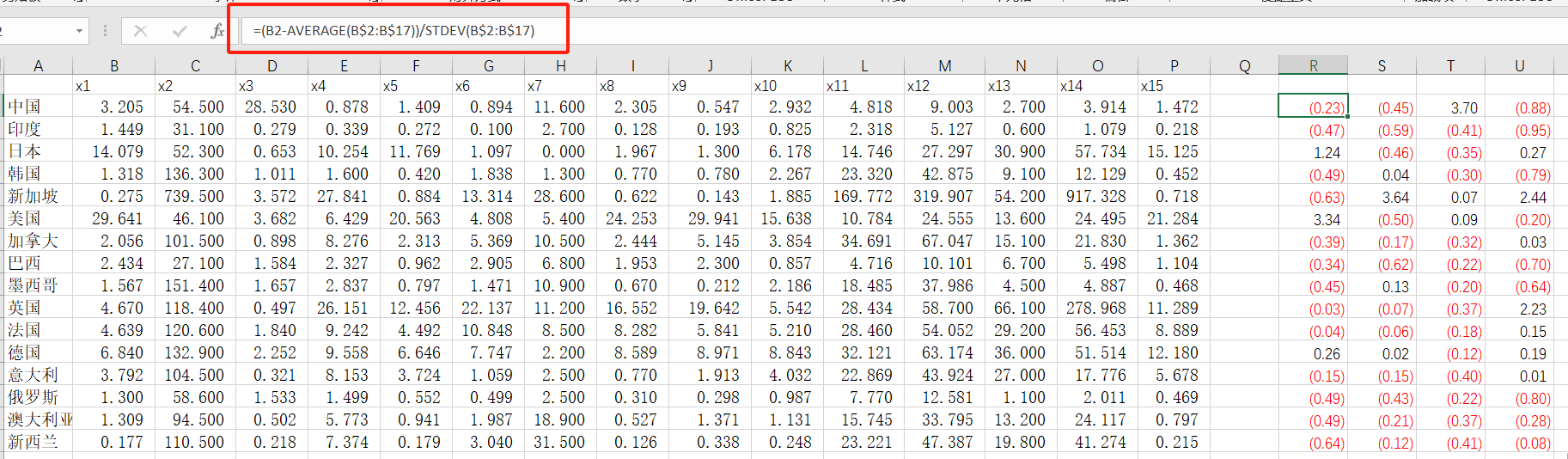
将成分矩阵的数据复制到Excel表中,重新计算主成分得分系数矩阵,公式为各成分的载荷除以各成分对应的特征值的算术平方根,即A/(sqrt(λ)。
.jpg)
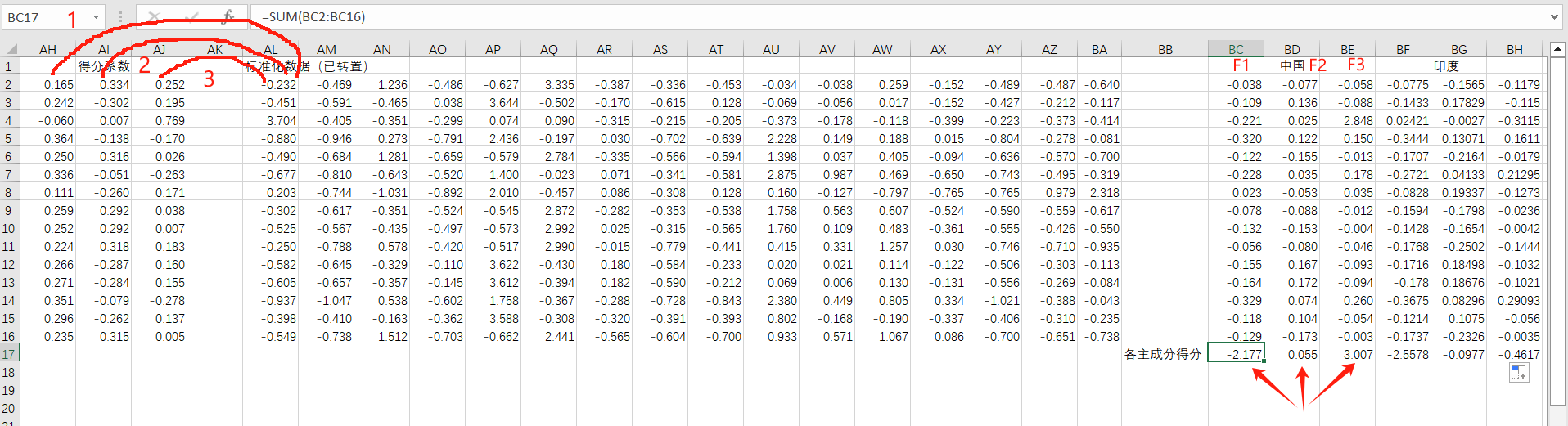
然后按下图将其与标准化后的原始数据一一对应相乘(标准化公式为(X-μ)/σ),得到真正的各主成分得分F1、F2、F3。
 |  |
更简单,也更常用的是
直接将spss的各项因子得分乘以对应主成分特征值的算术平方根也可转换为主成分得分(两者的公式差异)
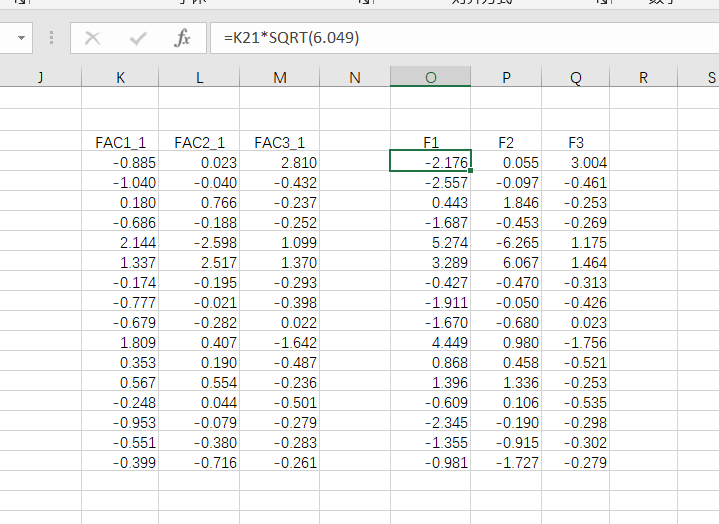
这里与下文的得分计算在第三位小数上存在差异,是因为代入数据只保留了三位小数而不是原始数据,这不影响最终结果
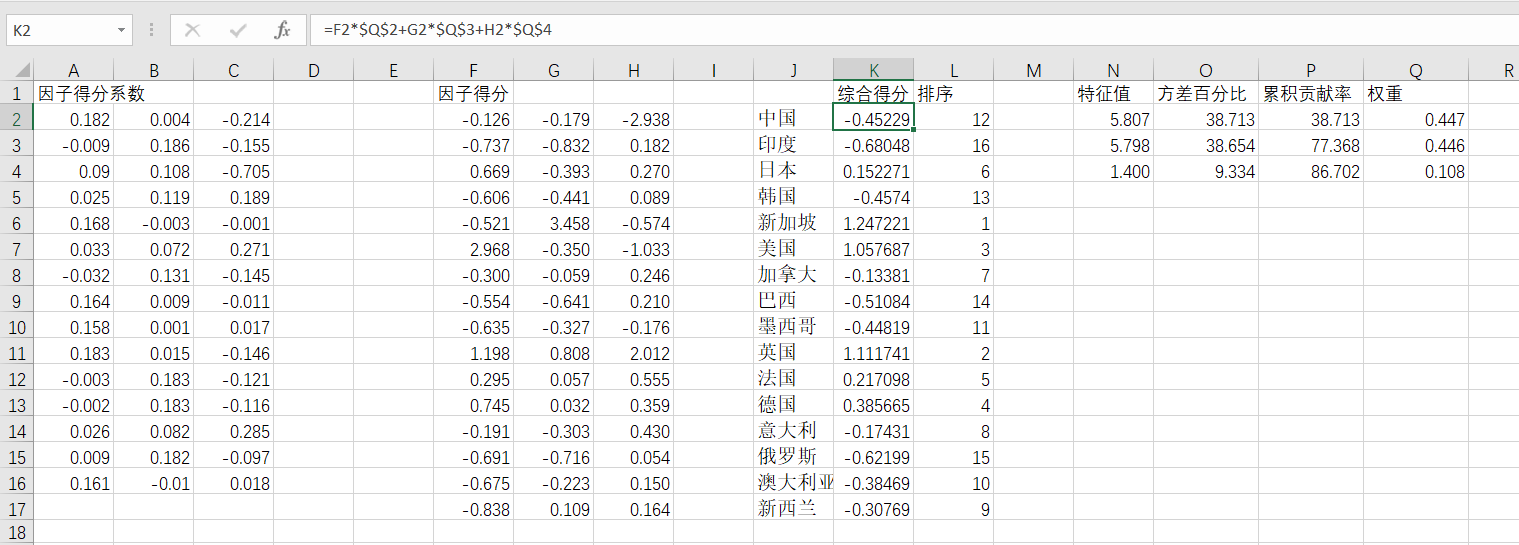
再根据权重计算主成分综合得分,这里权重计算公式为各主成分贡献率除以提取主成分的累积贡献率,最后进行排序。
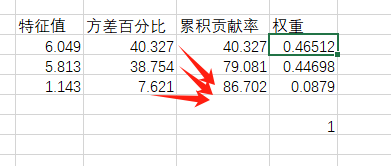 | 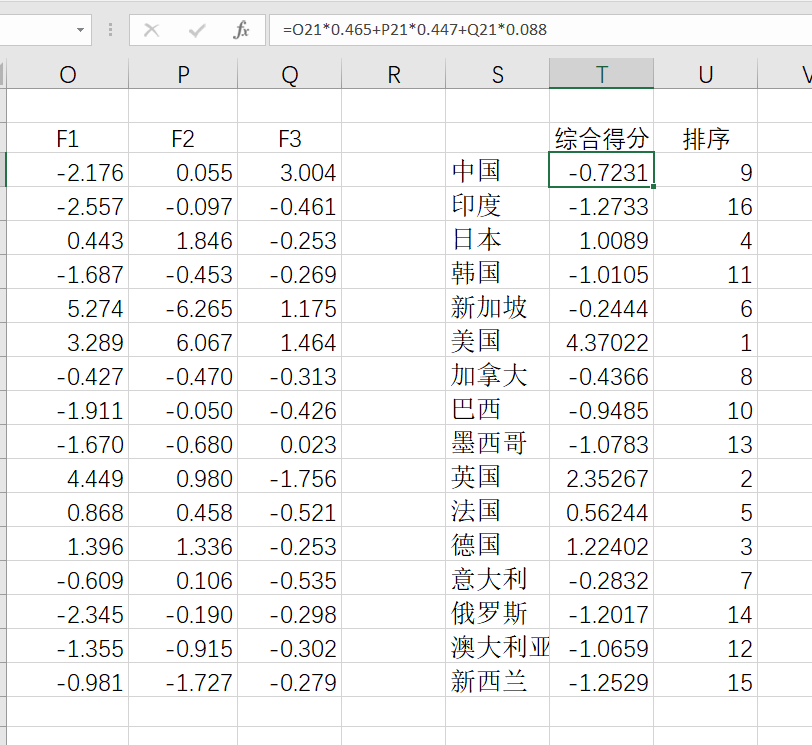 |
整理得出主成分得分表达式,式中y1、y2、y3中的每一项x的系数分别对应主成分1、2、3的成分得分系数(见上面Excel表中的F1、F2、F3),总表达式的各项系数对应w1、w2、w3(权重)
 |
|
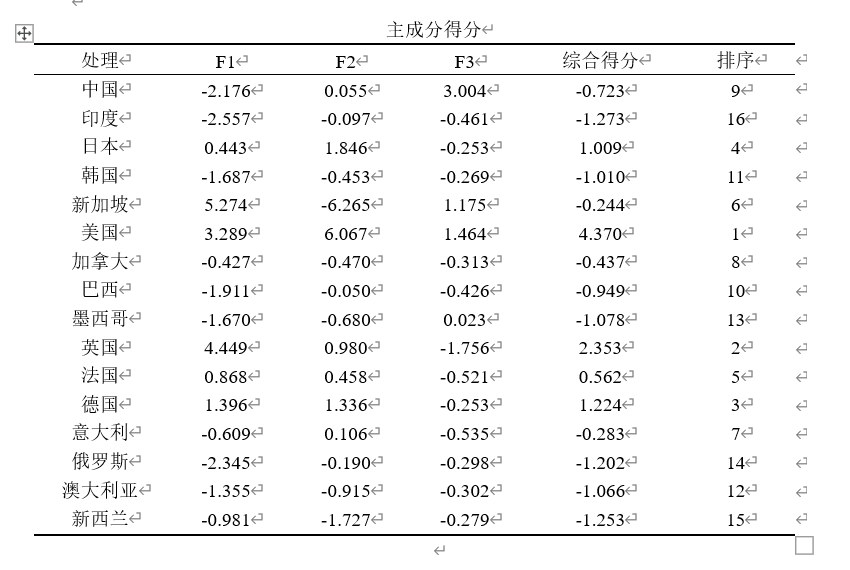 | |
以上分析结果与《主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷》一文相同。
SPSS因子分析操作
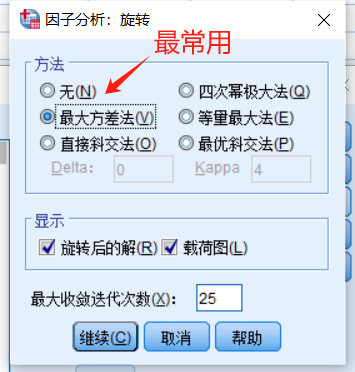
导入数据到spss中,点击spss上方的“分析”→“降维”→因子,将变量全移入到变量栏(与主成分分析操作一致),然后按下图操作。图2中方法选择“主成分”,其他方法还有未加权最小平方法、综合最小平方法、最大似然法、主轴因子法、Alpha因子法、映像因子法等等,最常使用的方法为主成分,最大似然法,主轴因子法。图3因子旋转的方法论文中常使用最大方差法(Varimax Method)。关于因子提取方法与旋转方法的选择可以参考因子分析:抽取 - IBM 文档与因子分析:旋转 - IBM 文档。
 |  |
 |  |
| |
首先看KMO与Bartllet检验,这里KMO<0.5,但通过了Bartllet检验,且公因子方差都接近1,相关性较好,表示还是可以进行因子分析的。(但一般都建议样本数远大于变量数,且通过KMO与Bartllet检验,这里是为了操作示范的方便,所以使用了主成分分析的数据)
.jpg) | 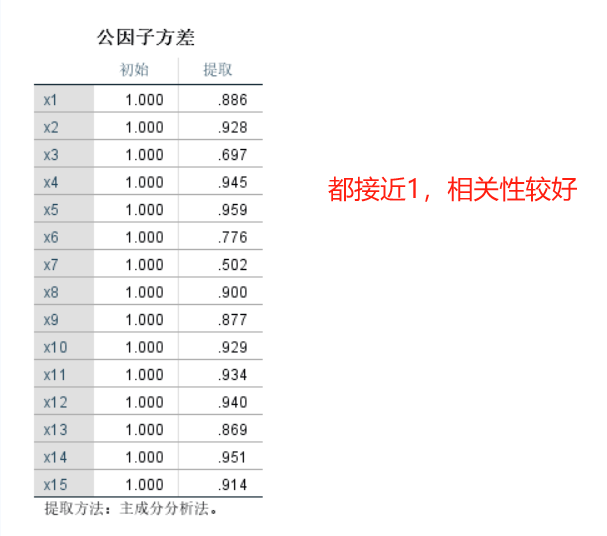 |
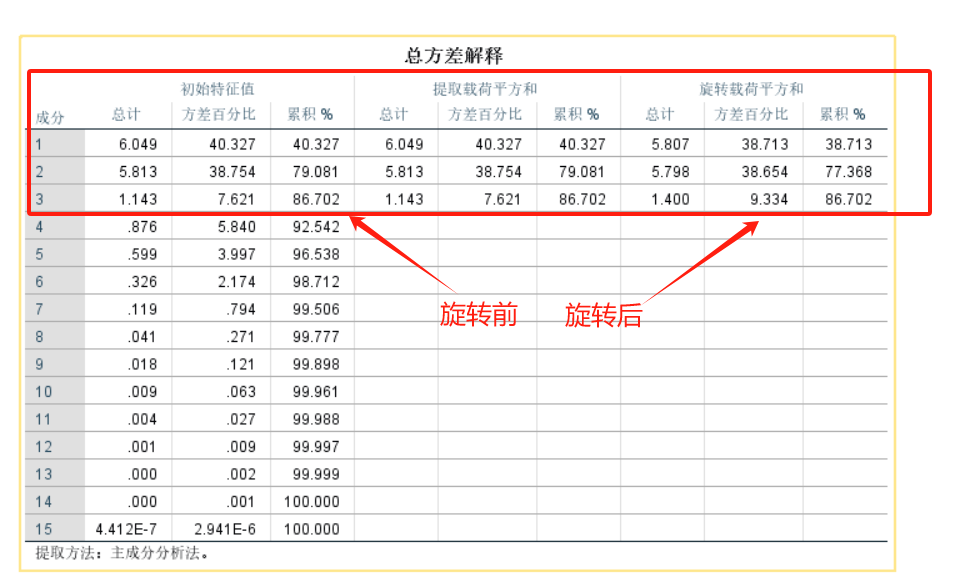
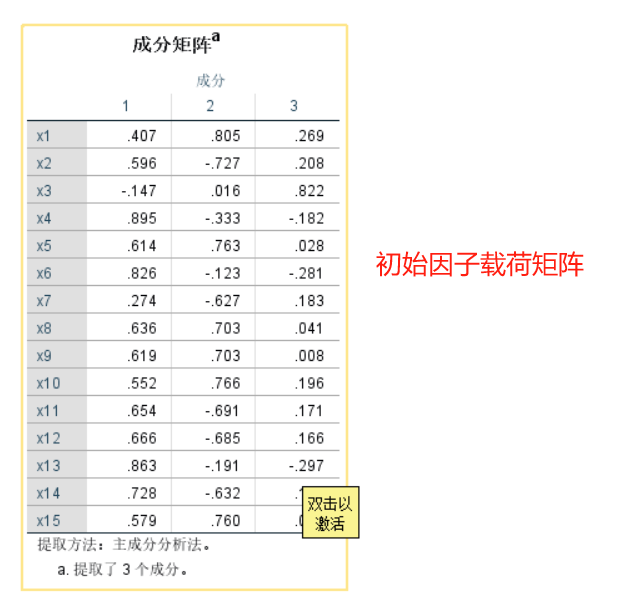
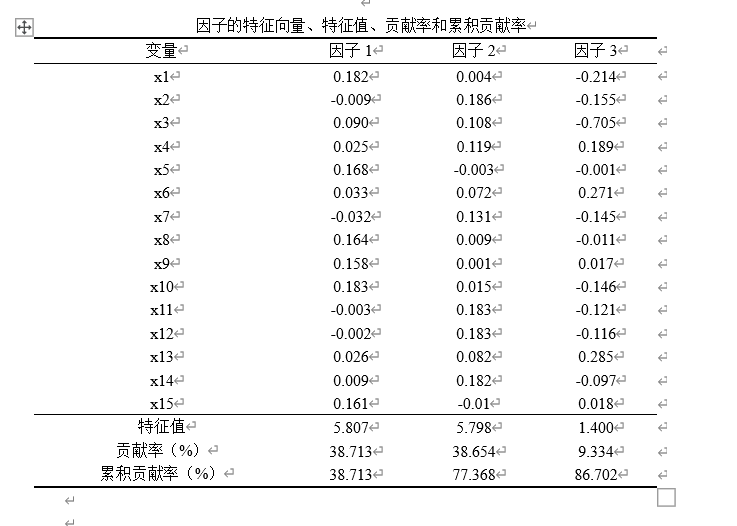
用SPSS进行因子分析十分方便,不必和主成分分析再进行额外的计算操作,直接可以得出结果。我们需要关注的主要数据为“总方差解释”,“成分得分系数矩阵”与“因子得分”。这里以特征值大于1且累计方差贡献率大于85%的标准(标准不固定,一般建议累积方差贡献率在85%以上,特征值大小为次要条件)来选择因子个数。如果提取因子的累计方差贡献率过低,可以再进行一次因子分析操作,在“提取“选项中选择“因子的固定数目”,然后自行确定因子个数来完成因子分析。本次分析中前三个因子的特征值均大于1,累计贡献率达86.702%,满足标准。碎石图也可以作为辅助手段,通过“拐点”来选择因子个数。
 |  |
 |  |
 | |
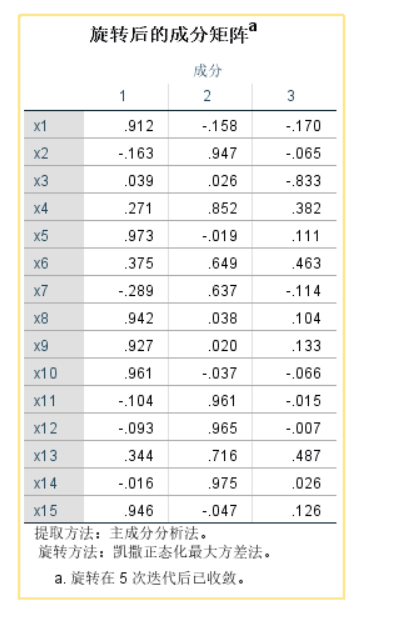
因子分析强调因子的可解释性,因子F1,F2,F3都是有实际的命名意义的,且最终结果与主成分分析相差较大。后续操作与上述主成分分析一致,得到因子分析结果。
 |  |
 | 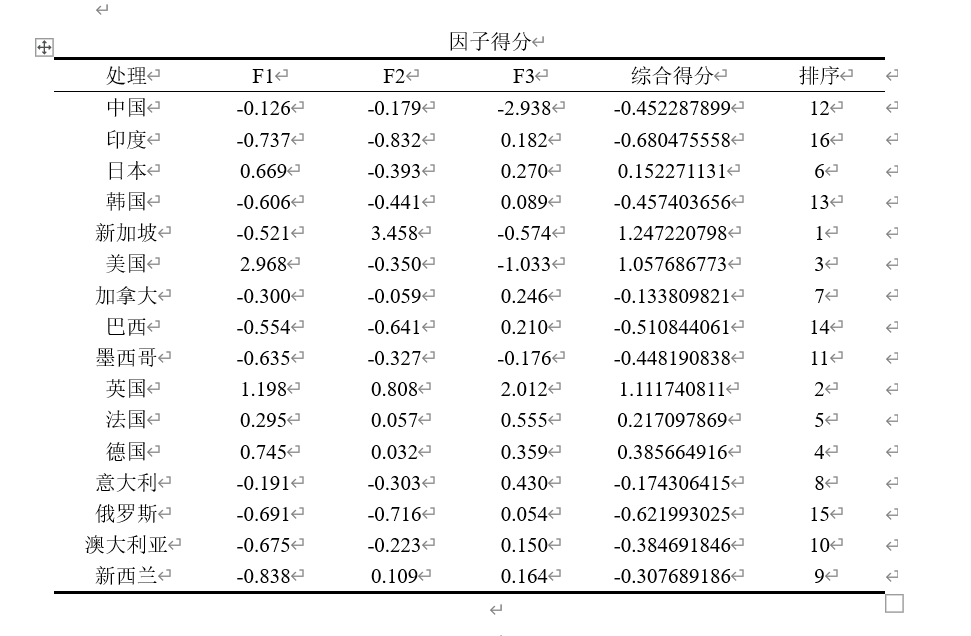 |
注意:样本数少于变量数,无法进行KMO与Bartllet检验;数据中出现缺失值会提示个案数不足,可以在‘’因子分析:选项‘’中勾选“替换为平均值”或者标为“0”;样本数过少时,如果某项变量各样本值都相似,也会提示个案数不足,可以考虑增加样本数或者删掉那项变量。

操作讲解结束,有什么问题欢迎评论区留言讨论!
参考资料
刘玉玫,张芃.经济全球化程度的量化研究[J].统计研究,2003,(12):13-18.
林海明,张文霖.主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J].统计研究,2005,(03):65-69.



.jpg)

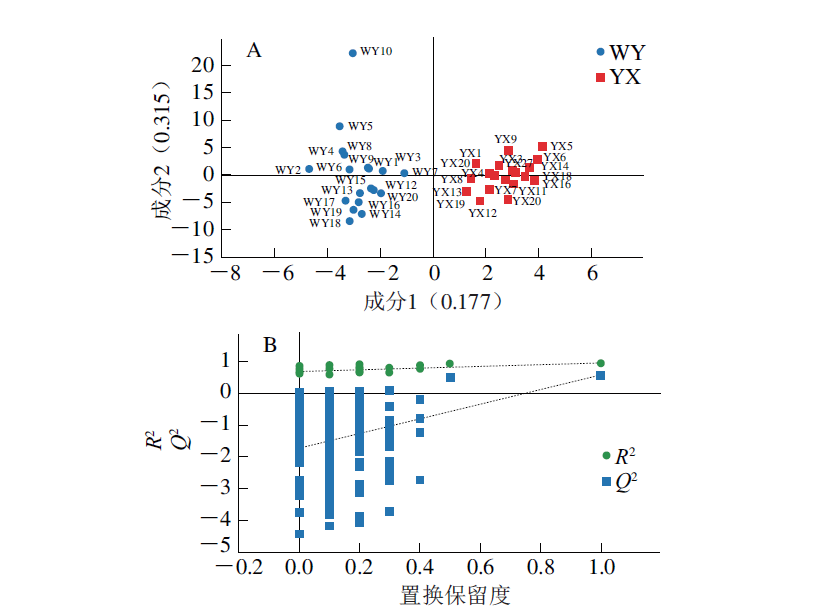

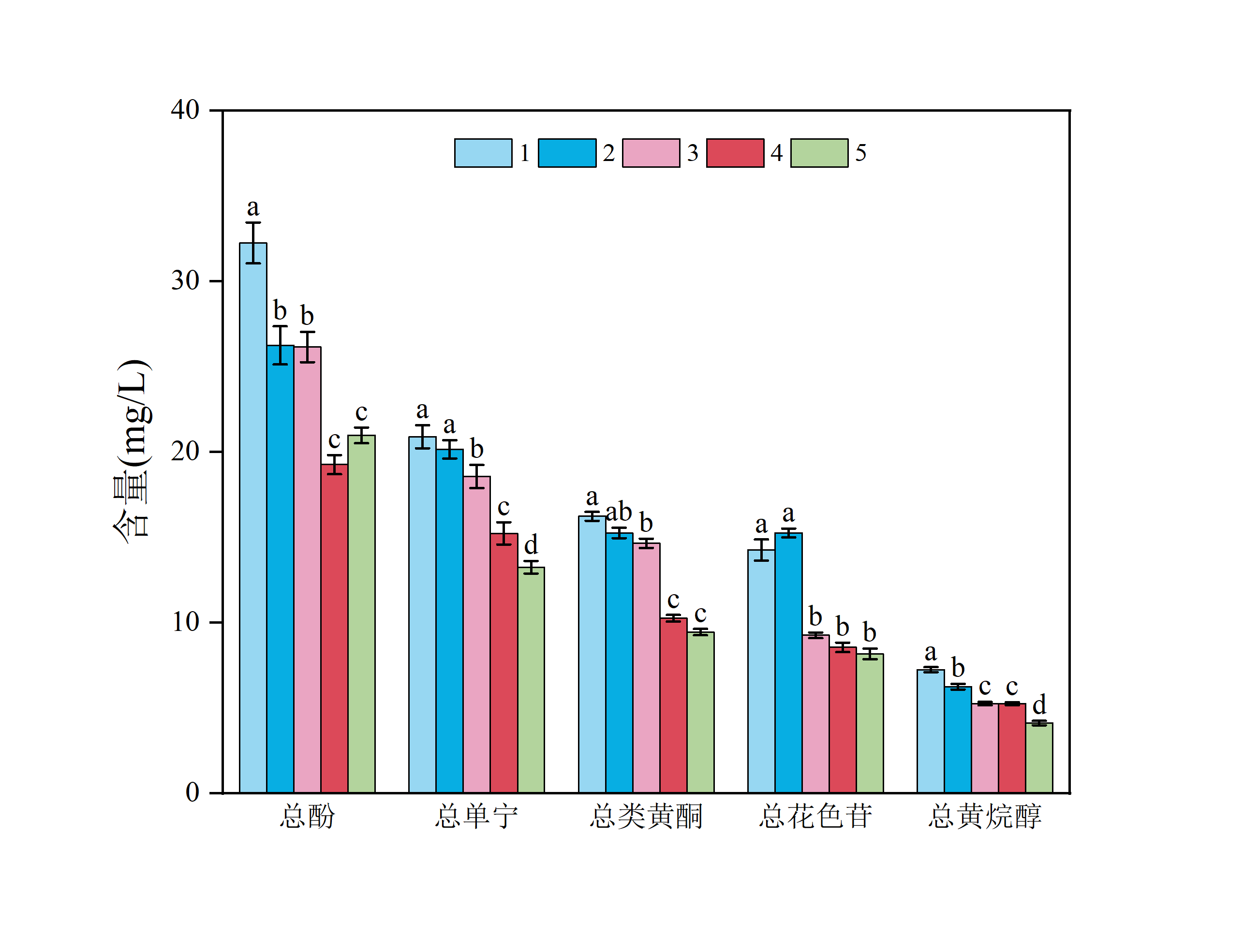
您好,我是胁迫试验,我是三个处理四个时期取样测定,每个三次重复,一个指标就是36个数据,测定十几个指标,我是把所有的数据输入spss,还是三次重复取均值呢?是直接输入吗不需要标准化吗,spss直接标准化吗?
求三次的平均值,输入原始数据就行,spss会自动标准化。
我昨天试了一下,发现我的样本量比标量少他没出来,说不是正定矩阵
正定矩阵的问题一个是你样本量少了(样本数低于指标数),另一个就是某几个指标的线性相关非常强,类似等比数列那种,解决办法就是合并线性相关强的指标。具体怎么合并看你的需求,比如酸度与pH这两个指标相关性强,你觉得酸度在评价指标中比较重要,那你就保留酸度,舍掉pH,基本不影响得分结果的。
一语点醒,非常感谢,就是我有11指标我刚刚试了一下主成分有4个这个多吗,
老师您好,就是我做的是盆栽试验,有十个处理,每个处理四个重复,然后测定了24个指标,如果要对这些指标进行主成分分析的话,需要先求处理内的平均值嘛,我的最终目的是想对这些处理进行一个综合排序,选最优处理
是的,按均值计算。
老师,您好。我想咨询下,就是我用白酒的风味数据做了主成分分析,但是奇怪的是您分析中说了用两种方式计算结果差异不大,但是我用我的数据照着您的步骤进行分析后,两种方法的计算结果不一致,相差还比较大,所以不太清楚是哪里出了问题,想询问下到底是巧合一样,还是方法没什么问题?
你指的是主成分得分那一部分的计算吗,具体你怎么计算的我这也不太清楚,但是两种方式的计算结果应该是一致的,你可以采用第二种方法,也就是“直接将spss计算的各项因子得分乘以对应主成分特征值的算术平方根转换为主成分得分”,这个不容易算错。
wyatt老师您好呀,想请教下您,利用主成分分析做综合评价的时候,需要考虑原始数据指标的方向性吗,期待您的解答,感谢三连😊😊😊
你好,一般来说是不用考虑原始数据指标的方向性的。但如果你的研究有明确的目的需求或方向倾向(比如评价企业的经济效益,那么净利润、利润率等可归于正向指标,负债率等可归于负向指标),则可以考虑方向性,通过改变某些指标的方向,使得主成分更具有可解释性与实际意义,综合评价结果也更容易理解,并且仍然属于客观赋权评价方法。
谢谢您的解答!